Mathematics can often feel like navigating a complex maze. You know the answer is there, but finding the right path can be challenging. The key isn't just knowing formulas; it's about having a toolkit of effective math problem solving strategies. Whether you're a primary school student tackling word problems, a senior student preparing for VCE or HSC exams, or a university student facing complex equations, mastering different approaches can transform frustration into achievement. The feeling of being stuck is universal, but the methods to get unstuck are learnable and powerful.
This article provides a curated roundup of eight proven strategies designed to build your problem-solving arsenal. We move beyond simple memorisation to focus on logical, repeatable processes that give you a clear plan of attack. Each section breaks down a specific technique, from classic frameworks like Polya's Four-Step Method to visual aids like drawing diagrams. You'll find practical examples tailored to different learning stages and actionable tips to help you implement them immediately. By the end, you'll have a versatile set of tools to confidently dismantle even the most intimidating mathematical challenges, turning obstacles into opportunities for success.
1. Polya's Four-Step Problem Solving Method
When faced with a complex maths problem, it's easy to feel overwhelmed and not know where to begin. The Polya method, developed by mathematician George Polya, is one of the most foundational and effective math problem solving strategies. It provides a reliable framework that organises your thinking into four distinct, manageable phases.
This systematic approach demystifies problem-solving by breaking it down into a logical progression. It's not about finding the answer instantly; it's about following a process that leads to a correct and well-understood solution. Adopted in curricula worldwide, from primary school to university engineering courses, its strength lies in its universal applicability.
The Four Steps to a Solution
Polya's method is built on a simple yet powerful sequence:
- Understand the Problem: Before you can solve anything, you must know exactly what is being asked. Identify the unknown, the given data, and the conditions. Rephrase the problem in your own words.
- Devise a Plan: Connect the data to the unknown. Have you seen a similar problem before? Consider strategies like drawing a diagram, looking for a pattern, working backwards, or writing an equation.
- Carry Out the Plan: Execute your chosen strategy step by step. Perform the necessary calculations and check each step for accuracy. Patience is key here; don't rush.
- Look Back: Once you have a potential answer, check if it's reasonable. Can you verify it? Can you derive the solution differently? This step helps catch errors and deepens your understanding.
This infographic simplifies the core workflow of Polya's method, focusing on the crucial progression from comprehension to verification.
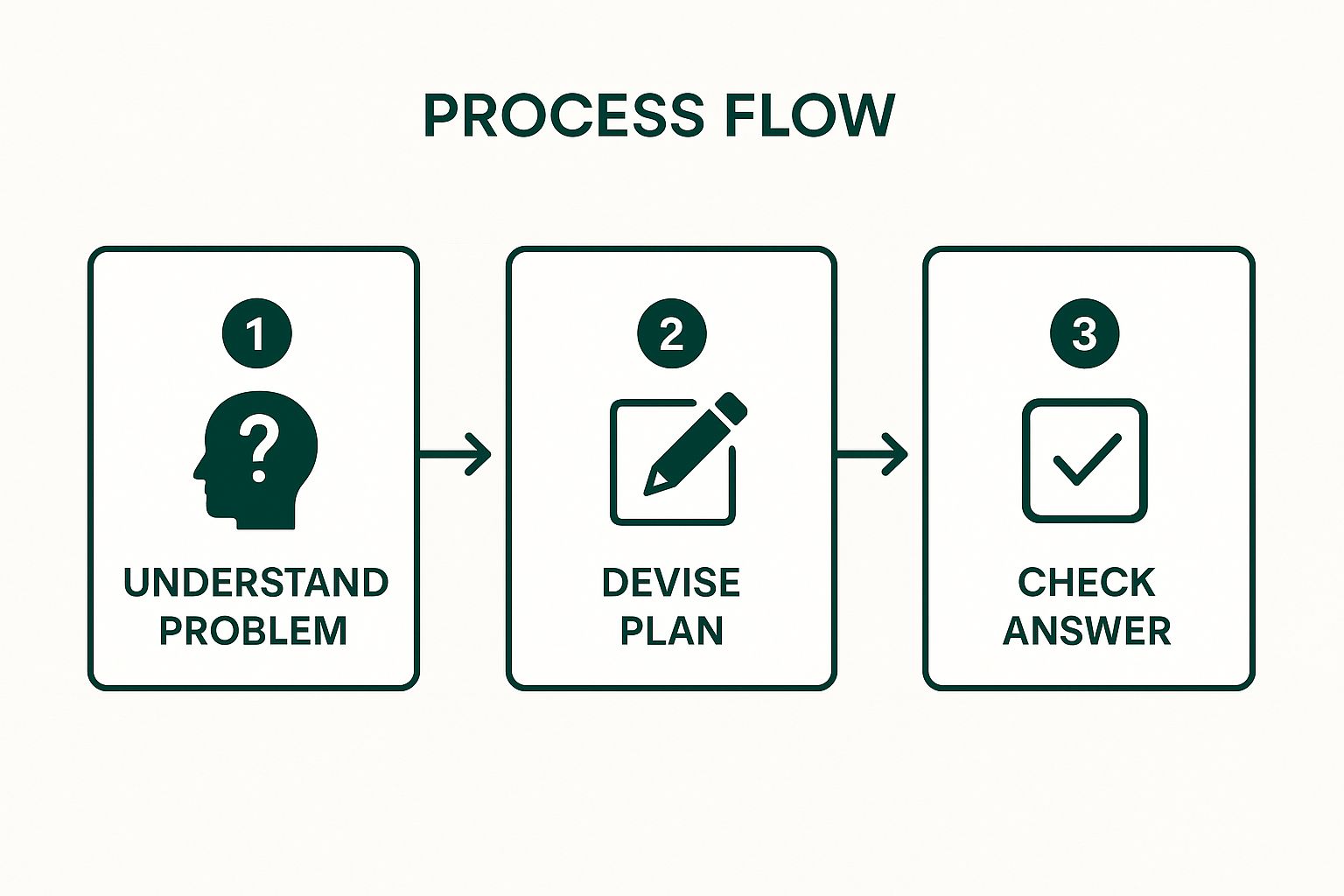
The visual flow emphasises that a successful plan is built on a solid understanding of the problem, and the final check is essential for confirming the result. By internalising this structured process, students can reduce anxiety, build confidence, and develop a methodical habit that ensures no critical step is overlooked.
2. Working Backwards Strategy
Some maths problems give you the final outcome and ask you to find the starting point. When the end is clear but the beginning is a mystery, the working backwards strategy is an incredibly powerful tool. This is one of the most effective math problem solving strategies for reversing a sequence of events or operations.
This approach flips the typical problem-solving process on its head. Instead of moving forward from a given starting point, you begin with the final result and undo each step in reverse order. It's particularly useful for problems involving a series of transformations, like calculating an original price after several discounts and taxes have been applied.
The Reverse Path to a Solution
The working backwards method is built on a logical reversal of operations:
- Identify the End Result: Clearly state the final value or condition given in the problem. This is your starting point.
- List the Steps in Reverse: Write down every operation or action described in the problem, but prepare to reverse them. For example, addition becomes subtraction, and multiplication becomes division.
- Undo Each Step: Starting from the end result, apply the inverse of each operation one by one, moving backwards toward the beginning.
- State the Initial Value: The number you are left with after undoing all the steps is your answer, the original value you were looking for. Always check your answer by working forward through the original problem.
This strategy helps make complex, multi-step problems more manageable by tackling one operation at a time. It removes the guesswork and provides a clear, methodical path to the solution. It is a fantastic method to use when preparing for exams, as it helps break down intimidating questions. For more study tips for exams, you can learn more about exam preparation strategies. By mastering this technique, students can confidently solve problems that might otherwise seem confusing or impossible to start.
3. Make a Table or Chart Strategy
When a maths problem presents a jumble of data, variables, or possible outcomes, it can be difficult to see the underlying relationships. The "Make a Table or Chart" approach is one of the most effective organisational math problem solving strategies for bringing clarity to chaos. It involves systematically arranging information into rows and columns, which helps visualise patterns and manage complex data sets.
This strategy transforms abstract or disorganised information into a structured, visual format. By organising data points logically, you can more easily track variables, identify trends, and ensure no possibilities are overlooked. This method is heavily emphasised in curricula like Singapore Math and by educators such as John Van de Walle because it builds foundational data-handling skills.

How to Implement This Strategy
Creating a useful table or chart involves a few key steps to ensure it effectively aids in solving the problem:
- Determine the Variables: First, identify what information needs to be tracked. These will become the headings for your columns and rows. For example, in a problem about distance, your columns might be 'Time', 'Speed', and 'Distance'.
- Set Up the Structure: Draw a grid and label your columns and rows clearly. A logical structure is crucial for making the data easy to interpret.
- Fill in the Data Systematically: Populate your table with the known information from the problem. Start with the simplest cases or the initial values given. As you calculate new data, add it to the table methodically.
- Analyse for Patterns: With the information neatly organised, look for relationships or patterns. Does one value increase as another decreases? Is there a constant ratio? The table makes these connections much easier to spot.
This structured approach is particularly useful for problems involving multiple scenarios, such as probability questions where you might list all possible outcomes. It is also invaluable for algebra, where function tables help in plotting graphs, or in statistics for recording and analysing data sets. By turning complexity into a clear visual map, this strategy empowers students to tackle multifaceted problems with confidence.
4. Look for a Pattern Strategy
The human brain is naturally wired to recognise sequences and repetitions. The 'look for a pattern' strategy leverages this innate ability, making it one of the most intuitive and powerful math problem solving strategies. This approach involves identifying recurring relationships, sequences, or structures within a problem to predict future outcomes or find a general solution.
Instead of tackling a large, complex problem head-on, you simplify it by examining smaller components to find an underlying rule. This method is particularly effective for problems involving sequences, geometric designs, or data sets that appear to follow a predictable progression. By identifying the core pattern, you can often develop a formula or algorithm that solves the entire problem efficiently.
How to Find and Use Patterns
Implementing this strategy requires observation and systematic thinking. The goal is to turn a series of observations into a generalised mathematical rule.
- Start with Simple Cases: Begin by solving the first few, simplest versions of the problem. For example, if asked for the 100th term in a sequence, calculate the first three or four terms first.
- Organise Your Data: Arrange your results in a table or list. This makes it easier to spot numerical, geometric, or algebraic patterns as they emerge. Look for common differences, ratios, or other relationships between consecutive terms.
- Formulate a Hypothesis: Based on your observations, create a rule or formula that describes the pattern. For instance, in the sequence 2, 5, 8, 11…, you might notice a common difference of 3.
- Test and Generalise: Verify your rule with another case or two. If it holds true, you can confidently apply it to find the required solution. This process builds logical reasoning skills that are foundational to higher-level mathematics.
By encouraging a systematic search for order, this strategy helps students develop a deeper appreciation for the structure of mathematics. If you're interested in building these foundational skills, you can learn more about engaging children with maths. This approach transforms daunting problems into manageable and often elegant solutions.
5. Draw a Picture or Diagram Strategy
Some maths problems can feel abstract and difficult to grasp, especially those described in words. The Draw a Picture or Diagram Strategy is a powerful visual approach that transforms complex information into a more concrete and manageable form. By creating a visual representation, you can often see relationships and solutions that weren't obvious from the text alone.

This method is one of the most versatile math problem solving strategies, applicable across nearly every area of mathematics, from basic geometry to advanced calculus. It helps bridge the gap between language and mathematical symbols, making it an essential tool for visual learners and anyone struggling to conceptualise a problem. Its value is recognised by leading educational bodies, including the National Council of Teachers of Mathematics.
Turning Words into Visuals
The core idea is to translate the problem's key elements into a simple, clear visual. This doesn't require artistic skill; a basic, well-labelled sketch is often more effective than a detailed drawing.
- Geometry: For problems involving shapes, area, or perimeter, drawing the figure is almost always the first step. It helps you visualise lengths, angles, and spatial relationships.
- Word Problems: A classic example involves motion. If two trains are travelling towards each other, a simple line diagram showing their starting points, directions, and speeds can make calculating the meeting point much simpler.
- Fractions and Ratios: Drawing models like fraction bars or pie charts can make operations like addition or finding a fraction of a whole number intuitive. For instance, visually dividing a rectangle into parts clarifies the problem.
- Set Theory: Venn diagrams are the standard for illustrating the relationships between different sets, making it easy to see overlaps and exclusions.
By externalising the problem onto paper, you free up mental resources to focus on the logic and calculations. A well-drawn diagram serves as a roadmap, guiding your steps and helping you organise information effectively, which is crucial for building confidence and achieving a correct solution.
6. Guess and Check (Trial and Error) Strategy
The Guess and Check method, often called trial and error, is a surprisingly powerful tool in the arsenal of math problem solving strategies. Far from being a random shot in the dark, this approach involves making an educated guess, checking it against the problem's conditions, and then using the result to inform and refine the next guess. It’s an interactive and intuitive process that builds understanding with each attempt.
This strategy is particularly effective for problems where the path to a solution isn't immediately clear, but you can easily verify if a potential answer is correct. By systematically testing possibilities, you can narrow down the range of potential answers and zero in on the correct one. Its strength lies in turning a complex problem into a series of manageable, testable steps, making it accessible even when formal algebraic methods seem too daunting.
How to Guess Systematically
The key to successful trial and error is organisation. A messy approach leads to confusion, while a structured one leads to a solution.
- Make an Educated Guess: Use the information in the problem to make a reasonable first guess. Don't pick a number at random; estimate a value that seems plausible.
- Check Your Guess: Substitute your guess into the problem to see if it satisfies all the given conditions.
- Analyse the Result: If the guess is wrong, determine how it is wrong. Was it too high or too low? Use this insight to make a smarter second guess.
- Repeat and Refine: Keep a neat record of your attempts. Continue the cycle of guessing, checking, and analysing until you arrive at the correct solution.
For example, when asked to find two numbers that have a sum of 20 and a product of 96, you could start by guessing two numbers that add to 20, like 10 and 10. Their product is 100 (too high). This tells you the numbers need to be further apart. Your next guess might be 8 and 12, whose product is 96. By analysing the failure of the first guess, you found the solution on the second attempt. This methodical process turns guessing into a genuine strategy.
7. Solve a Simpler Problem Strategy
When a maths problem seems impossibly large or abstract, one of the most powerful math problem solving strategies is to intentionally simplify it. The "Solve a Simpler Problem" approach involves breaking down a daunting question into a smaller, more manageable version that retains the core logic of the original.
This technique is about building momentum and uncovering patterns. By solving a simplified case, you can gain crucial insights into the underlying mechanics and relationships at play. This understanding can then be scaled up to tackle the original, more complex problem with confidence and a clear method. It is a cornerstone of mathematical thinking, championed by problem-solving experts like George Polya.
A Three-Step Guide to Simplification
The core idea is to reduce complexity without losing the essence of the problem. Here’s how to apply it:
- Identify and Simplify Key Elements: Pinpoint what makes the problem difficult. Is it large numbers, a complex geometric shape, or a long series? Replace these elements with their simplest possible forms, such as using the number 2 instead of 2,048, or a triangle instead of a dodecagon.
- Solve and Observe: Work through the simplified version of the problem. Pay close attention to the steps you take and the patterns that emerge in the solution. For instance, calculating compound interest for one or two years can reveal a pattern that applies to a 30-year period.
- Generalise and Apply: Use the pattern or method you discovered from the simpler problem to formulate a strategy for the original question. Your simplified solution acts as a blueprint, guiding you through the more complex calculations.
The real strength of this strategy lies in its ability to transform an intimidating challenge into an achievable one. It removes the initial mental block and provides a tangible starting point. Learning how to break down complex questions is a skill that makes even the most difficult problems accessible. This methodical approach builds not just the answer, but a deep, lasting comprehension of the mathematical principles involved.
8. Use Logical Reasoning Strategy
At its core, mathematics is the language of logic. The logical reasoning strategy is one of the most powerful math problem solving strategies because it involves a systematic process of deduction, moving step by step from known facts to a definitive conclusion. It's less about complex calculations and more about constructing a sound, sequential argument.
This method is crucial when a problem doesn't have an obvious numerical path but instead relies on relationships, conditions, and constraints. By applying principles of logic, you can eliminate impossible outcomes, identify necessary connections, and build a chain of reasoning that methodically uncovers the solution. It is particularly valuable in areas like geometry, algebra, and discrete mathematics.
How to Build a Logical Argument
Implementing this strategy involves transforming the problem into a series of logical steps. Here's a clear process to follow:
- Identify Givens and Goals: Start by clearly listing all the information provided in the problem (the "givens") and precisely what you need to find (the "goal"). This sets the foundation for your reasoning.
- Make Step-by-Step Deductions: Use the given information, along with established mathematical definitions and theorems, to make small, logical inferences. Each new conclusion should follow directly from the previous steps. For example, if you know a shape has four equal sides, you can deduce it is a rhombus.
- Eliminate Possibilities: In problems with multiple potential answers, use the conditions to systematically rule out options that are not logically possible. This is common in logic puzzles or problems involving constraints.
- Verify the Chain of Reasoning: Once you arrive at a solution, review your entire argument. Ensure that every step is logically sound and that no assumptions were made without justification.
This infographic highlights how logical reasoning bridges the gap between raw data and a proven solution, emphasising the importance of structured deduction.
The visual underscores that a conclusion is only as strong as the logical steps that support it. Mastering this strategy empowers you to tackle abstract problems with confidence, proving your answers rather than just finding them.
Comparison of 8 Math Problem Solving Strategies
| Strategy | Implementation Complexity | Resource Requirements | Expected Outcomes | Ideal Use Cases | Key Advantages |
|---|---|---|---|---|---|
| Polya's Four-Step Problem Solving Method | Moderate – requires disciplined step-following | Low – pen, paper, time | Systematic, verified solutions | Complex multi-step problems, proofs, word problems | Clear structure, builds critical thinking |
| Working Backwards Strategy | Low to moderate – reverse reasoning needed | Low – mainly cognitive effort | Efficient, direct solution paths | Algebraic equations, time/distance, known outcomes | Goal-oriented, reduces trial-and-error |
| Make a Table or Chart Strategy | Moderate – organizing data systematically | Medium – tools for tables/charts | Better data organization and pattern recognition | Data analysis, probability, combinatorics | Visual clarity, reduces cognitive load |
| Look for a Pattern Strategy | Moderate – requires observation and testing | Low – mainly thinking and paper | Logical insights, predictions | Number sequences, progressions, algebraic relations | Builds intuition, elegant problem solving |
| Draw a Picture or Diagram Strategy | Moderate – drawing skills and clarity needed | Low to medium – drawing tools | Enhanced understanding through visuals | Geometry, word problems, graphing, probability | Appeals to visual learners, clarifies problems |
| Guess and Check (Trial and Error) Strategy | Low – simple iterative process | Low – minimal tools | Approximate to exact solutions | Number problems, optimization, difficult algebraic equations | Accessible, builds estimation and persistence |
| Solve a Simpler Problem Strategy | Moderate – requires problem reduction skill | Low – time and cognitive effort | Manageable steps toward complex solutions | Complex word problems, advanced math, multi-step tasks | Reduces overwhelm, builds confidence |
| Use Logical Reasoning Strategy | High – demands strong logic and foundational knowledge | Low – mostly mental effort | Rigorous, reliable solutions | Proofs, logic puzzles, algebraic reasoning | Develops critical thinking, systematic approach |
Putting It All Together: Personalising Your Problem-Solving Toolkit
Navigating the world of mathematics can often feel like exploring a vast, uncharted territory. The eight powerful math problem solving strategies we've explored in this article, from Polya's foundational four steps to the intuitive process of drawing a diagram, are the essential tools in your explorer's kit. They are your compass, your map, and your climbing gear, each designed for a different type of challenge you might encounter. The goal isn't to memorise a rigid sequence of instructions, but to build a flexible and personalised mental toolkit.
Think of these strategies as different lenses through which you can view a problem. A complex algebra question might seem impenetrable until you try to Solve a Simpler Problem first. A word problem full of confusing details can suddenly become clear when you Draw a Picture or Diagram. The true power lies in recognising which tool, or combination of tools, is best suited for the task at hand. This ability to assess a situation and select the right approach is the hallmark of a confident and competent mathematician.
From Knowledge to Mastery
Simply reading about these methods is the first step; the journey to mastery is paved with active practice. The key takeaway is that problem-solving is a dynamic skill, not a static collection of facts. To truly internalise these techniques, you must apply them consistently and consciously.
Here are some actionable next steps to transform this knowledge into skill:
- Mix and Match: Take a single practice problem and attempt to solve it using two or three different strategies. Which one felt more natural? Which was more efficient? This exercise builds flexibility and deepens your understanding of each method's strengths.
- Reflect on Your Process: After solving a problem, take a moment to articulate why you chose a particular strategy. Was it because you recognised a pattern? Or did working backwards seem like the most logical path? This metacognitive practice is crucial for developing problem-solving intuition.
- Embrace the "Struggle": When you get stuck, resist the urge to immediately look for the answer. Instead, see it as an opportunity to deliberately switch strategies. This is where real learning happens, turning moments of frustration into breakthroughs in understanding.
Ultimately, strengthening your math problem solving strategies does more than just improve your marks. It cultivates critical thinking, enhances logical reasoning, and builds resilience, valuable skills that extend far beyond the classroom and into all aspects of life. By viewing each problem as a puzzle waiting to be solved, you transform mathematics from a daunting subject into an engaging and rewarding intellectual adventure. The confidence gained from conquering a difficult problem is a powerful motivator, proving that with the right toolkit, any challenge is surmountable.
Ready to build a truly personalised problem-solving toolkit for yourself or your child? The expert tutors at Evergreen Tutoring Services specialise in moving beyond memorisation to foster deep, strategic thinking. We help students identify and master the specific math problem solving strategies that unlock their potential, building lasting confidence and academic success. Visit Evergreen Tutoring Services to learn how one-on-one support can make all the difference.
Article created using Outrank










